Signed Integers

In the previous section, you learned how unsigned integers are represented in binary and how to convert between bases. But what about signed integers, those that can be either negative or positive? How are they represented? In the decimal number system, negative values are represented with the use of a special symbol, but the binary number system works with only two digits, 0 and 1. There are no symbols that can be used to represent a negative value. Instead, we must incorporate the sign of a value within the number itself using the bit values 0 and 1.

In this section, we explore two representations for encoding signed integers in the binary number system. When working with signed integers, we must know the size or unit of the binary value. For simplicity, the examples in this section all assume the values are stored or represented as a byte.

Signed Magnitude

A simple representation for storing signed numbers in binary is the signed-magnitude representation. In this representation, the left-most bit (referred to as the sign bit) stores the sign of the number, while the remaining bits represent the magnitude or absolute value of the number.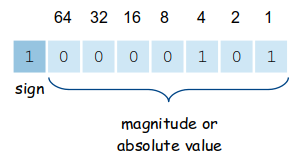

For example, -6 would be represented in 8-bits as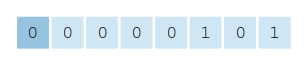

while +6 would be represented as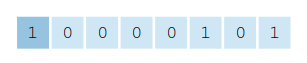

	Bit Terminology
	Given a fixed number of bits, the left-most bit of a binary number is referred to as the high-order bit or the most significant bit. The right-most bit is referred to as the low-order bit or the least significant bit.

Converting a signed-magnitude binary value to its decimal equivalent is rather simple. Suppose we want to convert the signed-magnitude binary value 10011001 to decimal:

Converting from a decimal value to its signed-magnitude equivalent is also a simple process. Follow the steps below to convert -39 to signed-magnitude using 8-bits:

As indicated earlier, when working with signed binary representations, we must know the binary unit size that will be used to store the signed value. What happens if the decimal value can not be represented in the given number of bits?

For example, suppose you are asked to convert -137 to its signed-magnitude 8-bit representation. The left most bit will be set to 1 since the value is negative

When the absolute value of 137 is converted to its unsigned binary representation, it will require 8-bits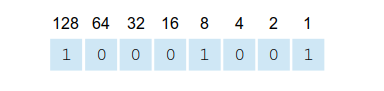

The final step is to take the bits of the absolute value and store them in the 7 remaining bits of the resulting binary representation. But decimal value 137 requires 8-bits to correctly represent it in binary. The 8th bit of the absolute value can not be stored in the signed-magnitude byte since the left-most bit represents the sign of the number.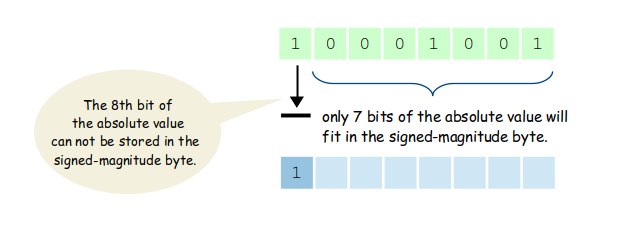

When a numerical value can not be represented in the given number of bits, the result is an overflow and the bits that overflow are discarded resulting in an incorrect value.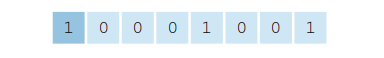

The signed-magnitude representation is a simple notation and the conversions between binary and decimal are easy to perform. But the signed-magnitude notation has two representations for the numerical value of 0: +0 and -0. This is a problem since the non-existent value of -0 would have to be dealt with in the circuits of the hardware when performing arithmetic on signed-magnitude values.

Two's Complement

A signed binary notation that corrects for the representation of the non-existent -0 is the two's complement notation. Like signed-magnitude, the left-most bit indicates the sign of the value, but in two's complement the left-most bit is part of the binary value itself.

Converting a decimal value to its equivalent in two's complementation notation is slightly more involved. Suppose we want to convert -83 to two's complement binary notation using 8-bits: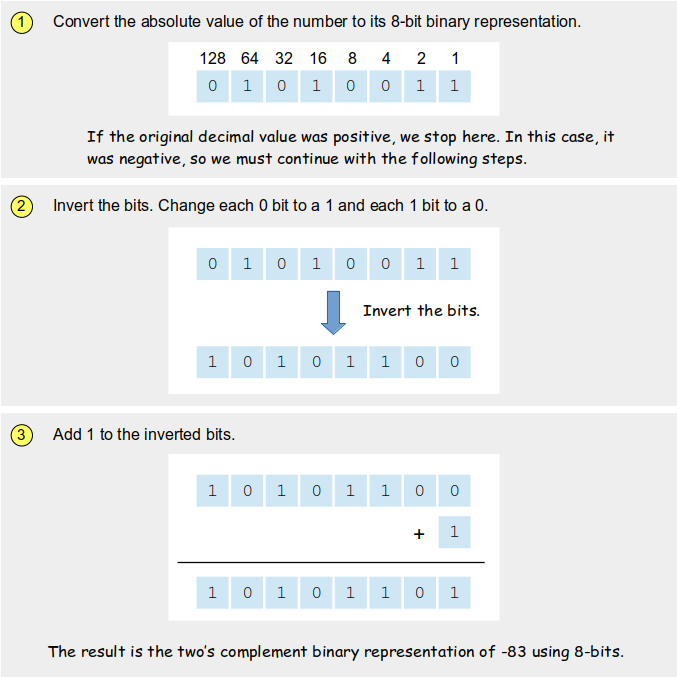

	Note
	If the value being converted is a positive number, then only the first step is performed. The steps that invert the bits and adds 1 are only performed when a negative value is converted.

Converting a two's complement binary value to its decimal equivalent is done using a similar process. If the two's complement value is positive (the sign-bit is 0), then covert it directly to decimal as you would with an unsigned binary value. If it is a negative value, then there are three steps to perform. Suppose we want to convert the two's complement binary value 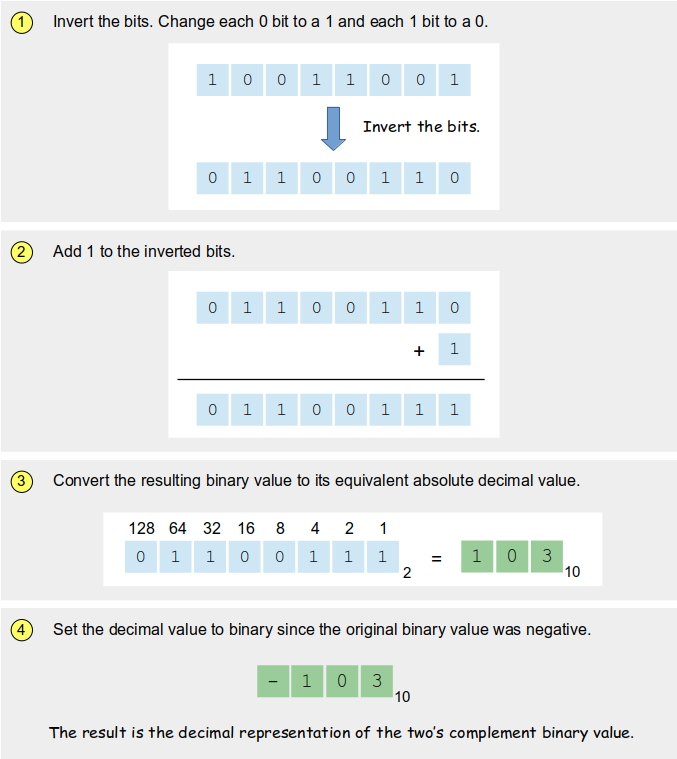10011001 to decimal:

As with the signed-magnitude notation, an overflow can occur when converting a decimal value to two's complement binary notation. This can be determined by checking the sign bit after the conversion. If the resulting sign bit is the opposite of the value being converted, then an overflow occurs. That is, an overflow occurs if:

• a positive number is being converted and the sign bit of the resulting value is a 1, or
• a negative number is being converted and the sign bit of the resulting value is a 0.

For example, suppose we convert -130 to two's complement notation using 8-bits. Following the steps from above, we convert the absolute decimal value (130) to binary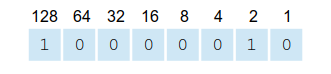

then invert the bits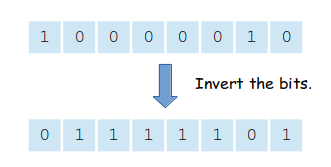

and add 1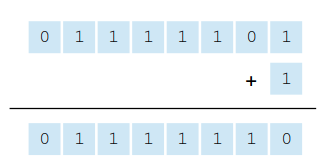

Notice that the sign bit of the resulting binary value is 0, but the original decimal value was negative. Thus, an overflow has occurred. The value that results from the conversion will be stored as is, even though it is not the correct value.

Signed Addition

Computers must also be able to perform arithmetic calculations with signed integers as well. The two's complement notation is implemented more efficiently at the logic circuit level than signed-magnitude. Thus, most modern computers using the two's complement notation. For that reason, we limit our discussion in this section to the use of two's complement binary values.

A major advantage of using two's complement notation to represent signed values in binary is the simplicity of addition and subtraction. Adding two signed binary values represented in two's complement is done the same way as two unsigned values.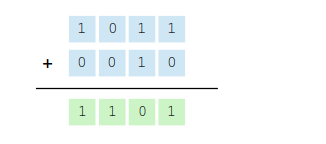

We can again verify the result by converting each binary value to its decimal equivalent and adding the decimal values: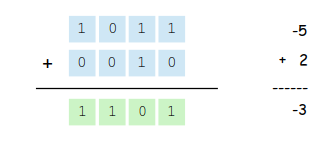

Subtraction is performed using addition. To subtract one value from another, we negate the value that we want to subtract and then add the two values. This eliminates the need to "borrow" from the right column. For example, suppose we want to compute the following subtraction in binary

which is the same as adding 97 and -15. The example below illustrates the subtraction using 8-bits.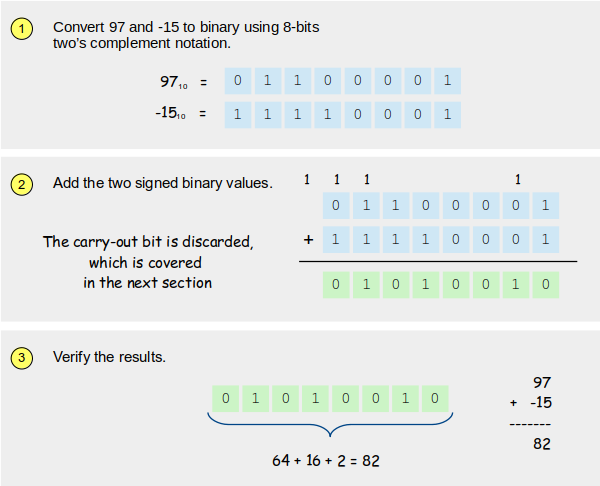

	Note
	It is important to note that when adding two binary values, both values must be represented in the same notation. That is, both values must be unsigned or both must be signed using the two's complement notation. We can not mix the types.

When adding two signed binary values represented in two's complement notation, a carry-out beyond the left bit does not determine overflow. Instead, an overflow occurs if:

• the sum of two positive numbers yields a negative result
• the sum of two negative numbers yields a positive result.

That is, if the two values being added have the same sign (positive or negative) and the result is the opposite, then an overflow has occurred. If there is a carry-out bit when adding two signed values, the extra bit is simply discarded. Discarding the bit does not alter the result as it does when adding two unsigned values.

Below are three examples of binary addition with two's complement values, two with an overflow and one without.