Binary Numbers

Computers represent numerical values as binary numbers, which are expressed in the base-2 numerical system or binary number system. The binary number system represents values using only two symbols: 0, and 1. In this section, we will examine binary numbers and learn how to convert between the binary system used by computers and the decimal system preferred by humans.

Basic Units

Computers work with different units of binary values. The smallest unit is a single digit of 0 or 1, which is called a bit or binary digit. Larger units are created by forming groups or sequences of bits the same way we do in the decimal number system. A sequence of 8 bits is called a byte. This is the smallest unit that machine code instructions typically work with and it represents the smallest unit of addressable memory storage on most computers. Although not common today, a byte can be divided into two 4-bit values, called nibbles.

A word consist of 16 or more bits, but the actual size depends on the specific architecture. A word represents the number of bits that a computer natively works with when carrying out operations on the ALU or transmitting data across the system bus. A computer with a 32-bit architecture, like most PCs until recently, has a word size of 32 bits. A 64-bit architectures has a word size of 64 bits. Some computers can also work with a half word, which as indicated by its name is half the size of a word on a given computer.

Positional Numbering System

At some point in grade school, you learned that decimal numbers are represented as a positional numbering system in which a numerical value is represented through increasing powers of its base (10):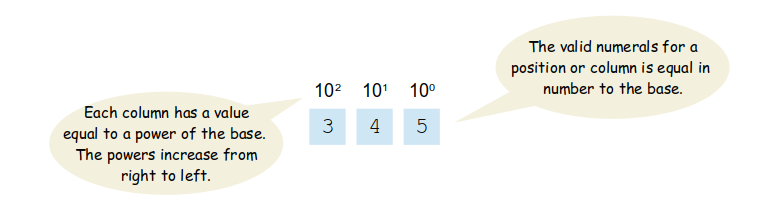

In a positional numbering system, the value of a numerical representation is determined by summing the product of each column value and the numeral in that column: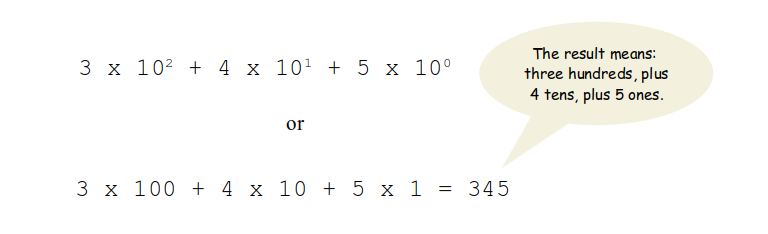

Any base can be used to create different number systems. The binary number system is a positional numerical system that uses a base of 2.

As a computer scientist it will be important for you to understand and be able to work with the binary number system. While there is not much call for binary numbers when working with a high-level language, there are many problems in and areas of computer science that rely on this knowledge. In addition, it is important that you understand how the computer executes programs and processes data, all of which is stored as binary values.

In the following sections, you will learn how to convert numbers between the decimal and binary number systems. Converting small values is rather simple, but larger values usually requires a calculator or pencil and paper. We will begin with converting unsigned numbers (those that are non-negative). Working with and converting signed numbers (those that can be positive or negative) is more complex and will be discussed in the next section.

Binary to Decimal Conversions

Converting an unsigned binary value to decimal is rather simple. Suppose we want to convert the 8-bit binary value

to its decimal equivalent. Remember, the binary number system is a positional number system. That is, each column has a value that is a power of 2

which can also be written as

To compute the equivalent decimal value, simply sum the column values for each column that contains a 1 and ignore those that contain a 0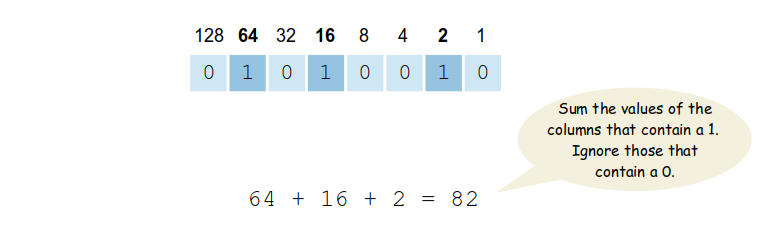

Question 3.

Convert the following binary values to their decimal equivalent:

1.   1 0 1 0 0 1 1 1 

2.   0 1 1 1 1 0 0 0 

1. 167 which is derived by summing the column values: 128 + 32 + 4 + 2 + 1 = 167.
2. 120 which is derived by summing the column values: 64 + 32 + 16 + 8 = 120.

Decimal to Binary Conversions

Given a decimal value, we can convert it to a binary value using a simple algorithm:

• Determine the base 2 column values that add up to the given decimal value.
• Place a 1 in those columns and a 0 in the remaining columns.

But how do we determine the column values that add up to the given value? Suppose we want to convert 203 to its equivalent in binary. Follow the steps illustrated below to see how the conversion is performed:

Computers work with a fixed number of bits, depending on the given data type. Thus, when converting from decimal to binary, you typically use a fixed number of bits, such as 8, 16, or 32. If you are not told the number of bits to use, you should use the minimum number of bits necessary to represent the given value.

Example

Convert 385 to Binary

Problem: Assume a binary unit size of 16 bits and convert the decimal value 385 to its binary equivalent. Solution: Using the steps outlined above, you will find that the following column values in the binary system add up to 385 in the decimal system: Since we are to assume a unit size of 16 bits for the binary value, we must also add zeros to the columns preceding the first bit containing a 1.

Question 4.

Convert the following decimal values to their binary equivalent. Assume a unit size of 8-bits.

1. 19
2. 175

1. 0 0 0 1 0 0 1 1

   which is obtained by adding the binary column values of 16 + 2 + 1 = 19.

2. 1 0 1 0 1 1 1 1 which is obtained by adding the binary column values of 128 + 32 + 8 + 4 + 2 + 1 = 175.

Question 5.

Convert the following decimal values to their binary equivalent. Assume a unit size of 16-bits.

1. 683
2. 255

1. 0 0 0 0 0 0 1 0 1 0 1 0 1 0 1 1

   which is obtained by adding the binary column values of 512 + 128 + 32 + 8 + 2 + 1 = 683.

2. 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 which is obtained by adding the binary column values of 128 + 64 + 32 + 16 + 8 + 4 + 2 + 1 = 255.

Binary Addition

Computers must be able to perform arithmetic calculations on integer values. Binary addition of unsigned values is carried out in the same way that humans add decimal numbers using pencil and paper.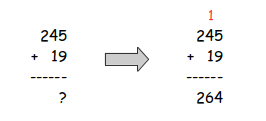

The major difference is that instead of carrying power of ten to the next column, we carry a power of two. There are four possible conditions when adding individual columns of binary integers: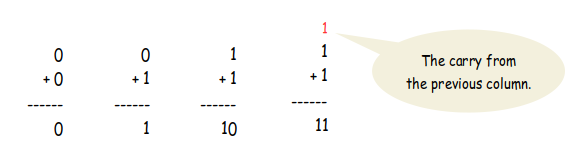

To illustrate, suppose you are asked to add two unsigned 8-bit binary values: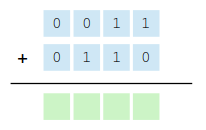

Follow the steps below to see how the addition is performed.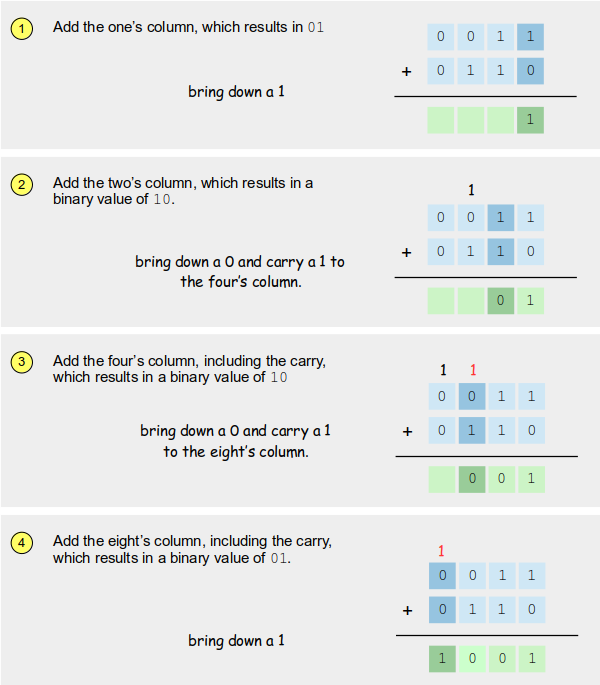

We can verify this result by converting each binary value to its decimal equivalent and adding the decimal values: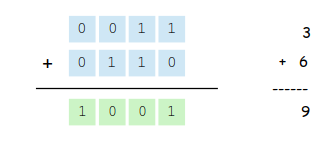

When a computer works with binary values, they are represented in a fixed number of bits (i.e. unit size). When converting from decimal to binary or adding binary values, an overflow can occur. When adding two unsigned binary values, an overflow occurs if there is a carry-out beyond the left bit.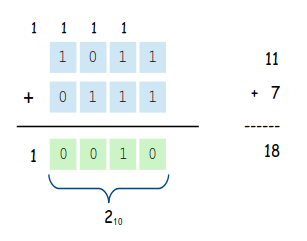

When an overflow occurs, the extra bit is dropped, thus resulting in an incorrect value. Although, 10010 is the actual result of adding the two values, 0010 will be the value that results from the addition since we are using a 4-bit unit.

Question 7.

Add the following binary values stored as bytes.

    0 0 1 0 0 1 1 1
  + 0 1 0 1 0 1 1 0
 -------------------

The addition is performed as follows:

            1 1 
    0 0 1 0 0 1 1 1
  + 0 1 0 1 0 1 1 0
 -------------------
    0 1 1 1 1 1 0 1

which results in a value of 0 1 1 1 1 1 0 1.

Question 8.

Add the following binary values stored as bytes.

    0 1 1 1 1 0 0 0 
  + 0 1 1 0 1 0 1 1
 -------------------

The addition is performed as follows:

    1 1 1 1        
    0 1 1 1 1 0 0 0 
  + 0 1 1 0 1 0 1 1
 -------------------
    1 1 1 0 0 0 1 1

which results in a value of 1 1 1 0 0 0 1 1 .

Question 9.

Add the following binary values stored as bytes.

    1 1 0 0 1 0 0 1 
  + 0 1 1 1 1 0 1 1
 -------------------

The addition is performed as follows:

  1 1 1 1 1   1 1         
    1 1 0 0 1 0 0 1 
  + 0 1 1 1 1 0 1 1
 -------------------
    0 1 0 0 0 1 0 0    

which results in an overflow and a value of 0 1 0 0 0 1 0 0.