| Books and References © Rance Necaise |
|
|
Hexadecimal RepresentationWhen dealing with numerical values, humans prefer to work with the familiar decimal notation. But computers work with values in binary notation and sometimes we have to work with those as well. Specifying values in binary notation, especially when they consist of 32-bits or more 01011010011100110010110011100110 can be tedious and error prone. Instead of working directly with binary values, however, we typically specify values in a third positional numbering system. The hexadecimal number system is a base 16 system that allows for easy translation with binary values. As a positional system, each column has a value that is a power or 16: 
and each column can have one of 16 different numerals as illustrated in Table 1. The first ten numerals are the same as those used with decimal values (0 - 9) and the remaining six numerals correspond to the letters
Table 1. The 16 digits in the hexadecimal number system.
In computer science, hexadecimal notation is typically used to specify binary values in a high-level language without having to write all of the bits. It is also widely used with assembly languages and machine code. Thus, in this section, we limit our focus to the number conversions between binary and hexadecimal values only. Hexadecimal to BinaryConverting a hexadecimal value to its binary equivalent is a rather simple process. We simply convert each digit in the hexadecimal value to its equivalent 4-bit binary value, which are listed in Table 2 for easy reference.
Table 2. The 16 hexadecimal digits and their corresponding binary values.
To illustrate the process, suppose we want to convert the value 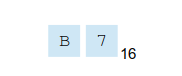
Each hexadecimal digit will be converted to a 4-bit binary value for a total of 8 bits. 
Each 4-bit binary value will take the same relative position as the corresponding hexadecimal digit in the original hexadecimal value. 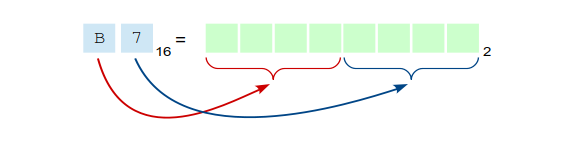
We start with the right-most digit and work our way to the left, one digit at a time. The 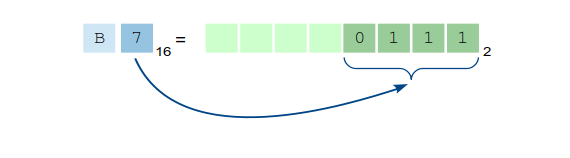
The next digit is 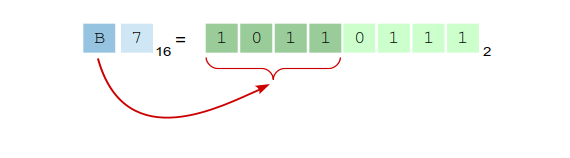
The end result is a binary value of 
Binary to HexadecimalThe reverse conversion can be performed in a similar fashion. Suppose we want to convert the 16-bit value 01101101111100102
to its hexadecimal equivalent. Follow the steps illustrated below to see how the conversion is performed: 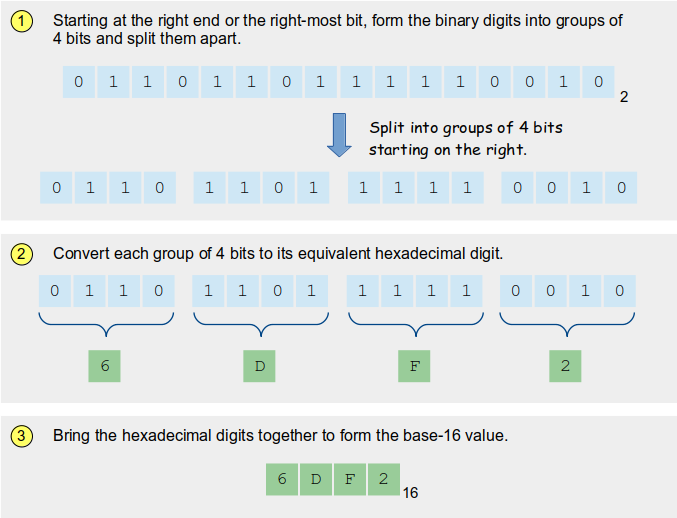
Question 1.
Convert each of the following numerical values to the indicated numbering system. When entering an answer in hexadecimal, enter hexadecimal letters in uppercase.
Question 2.
Convert the original 32-bit binary value example 01011010011100110010110011100110 to its equivalent hexadecimal value. The 32-bit binary value will result in the 8-bit hexadecimal value 5A732CE6 which was derived by: 1) splitting the 32 bits into groups of 4 starting on the right: 0101 1010 0111 0011 0010 1100 1110 0110 2) converting each 4-bit group to its equivalent hexadecimal value 0101 1010 0111 0011 0010 1100 1110 0110 5 A 7 3 2 C E 6 3) pushing the hexadecimal digits together to form the 16-base value.
|